1. Khi nào sử dụng?
Cronbach’s alpha là thước đo phổ biến nhất của tính nhất quán bên trong. Nó thường được sử dụng nhất khi bạn có nhiều câu hỏi Likert trong một cuộc khảo sát / bảng câu hỏi tạo thành một thang đo và bạn muốn xác định xem thang đo đó có đáng tin cậy hay không.
Đầu tiên, độ tin cậy là gì? Giả sử một cá nhân tham gia khảo sát về mức độ hạnh phúc. Điểm số hạnh phúc của bạn sẽ có độ tin cậy cao (nhất quán) nếu nó tạo ra kết quả giống nhau hoặc tương tự khi cùng một cá nhân thực hiện lại cuộc khảo sát của bạn, trong cùng điều kiện. Tuy nhiên, giả sử một cá nhân, ở cùng mức độ hạnh phúc thực sự, thực hiện khảo sát hạnh phúc này hai lần liên tiếp và một điểm cho thấy mức độ hạnh phúc cao và điểm số còn lại cho thấy mức độ hạnh phúc thấp – thước đo đó sẽ không đáng tin cậy chút nào.
Cronbach’s alpha cho chúng ta một cách đơn giản để đo lường xem một điểm số có đáng tin cậy hay không. Nó được sử dụng với giả định rằng bạn có nhiều mục (Item) đo lường cùng một cấu trúc cơ bản: vì vậy, đối với khảo sát về mức độ hạnh phúc, bạn có thể có tất cả năm câu hỏi, X1, X2, … X5, hỏi về những thứ khác nhau, nhưng khi kết hợp lại, có thể được coi là để đo lường mức độ hạnh phúc tổng thể.
Cronbach’s alpha có một số hạn chế: các điểm số có số lượng thấp của mục (Item) liên quan với chúng có xu hướng có độ tin cậy thấp hơn và kích thước mẫu cũng ảnh hưởng đến kết quả của bạn tốt hơn hoặc xấu hơn. Tuy nhiên, nó vẫn là một thước đo được sử dụng rộng rãi, vì vậy nếu hội đồng của bạn đang yêu cầu bằng chứng rằng công cụ của bạn là nhất quán nội bộ hoặc đáng tin cậy, thì Cronbach’s alpha là một cách tốt để thực hiện!
2. Các tiêu chuẩn và diễn giải Cronbach’s Alpha
Về mặt lý thuyết, kết quả Cronbach’s alpha sẽ cho bạn một số từ 0 đến 1, nhưng bạn cũng có thể nhận được số âm. Một số âm cho biết có điều gì đó không ổn với dữ liệu của bạn — có lẽ bạn đã quên tính điểm một số mục. Quy tắc chung là hệ số Cronbach’s alpha từ 0.70 trở lên là tốt, 0.80 trở lên là tốt hơn và 0.90 trở lên là tốt nhất. Một thang đo là đạt được độ tin cậy nếu thỏa mãn 2 tiêu chí chính (có thể xem xét thêm 1 tiêu chí phụ) ở dưới đây:
– Theo Cortina, một hệ số “Cronbach’s alpha” tổng thể của nhóm là cao hơn ‘0.7‘ thực sự phản ánh tính nhất quán nội bộ, bất kể số lượng phản hồi [1].
– Nếu một mục (Item) có hệ số tương quan biến – tổng ‘Corrected Item – Total Correlation’ ≥ 0.3 thì mục đó đạt yêu cầu và giữ lại. Nếu phát hiện Item nào nhỏ hơn 0.3 thì chúng ta loại bỏ mục đó và chạy lại Cronbach’s alpha.
– Tiêu chí phụ, giá trị của cột Cronbach’s Alpha if Item Deleted cho biết hệ số Cronbach’s Alpha mới của nhóm nếu biến đang xem xét bị loại bỏ. Nếu các giá trị Cronbach’s Alpha if Item Deleted nhỏ hơn hệ số Cronbach Alpha tổng thể của nhóm thì chúng ta chấp nhận và giữ lại các mục trong nhóm. Ngược lại, nếu giá trị Cronbach’s Alpha if Item Deleted (tại Item 3) lớn hơn hệ số Cronbach Alpha tổng thể của nhóm thì chúng ta nên cân nhắc xem xét Item này tùy vào từng trường hợp.
+ Nếu Cronbach’s Alpha của nhóm ≥ 0.7 và hệ số tương quan biến – tổng ‘Corrected Item – Total Correlation’ ≥ 0.3 thì chúng ta giữ lại ‘Item 3’, không cần quan tâm đến giá trị Cronbach’s Alpha tương ứng với việc loại bỏ nó là bao nhiêu.
+ Nếu Cronbach’s Alpha của nhóm < 0.7, hệ số tương quan biến – tổng ‘Corrected Item – Total Correlation’ ≥ 0.3 và giá trị Cronbach’s Alpha mới nếu ‘Item 3’ bị loại bỏ là lớn hơn 0.7 thì chúng ta xóa bỏ Item 3 khỏi thang đo và chạy lại Cronbach’s Alpha để đạt được độ tin cậy.
+ Nếu việc loại bỏ ‘Item 3’ nhưng thang đo vẫn không đủ tiêu chuẩn. Khi đó, thang đo không đảm bảo độ tin cậy cho nghiên cứu, cần loại bỏ cả thang đo này.
+ Nếu sự chênh lệch giữa Cronbach’s Alpha của nhóm với Cronbach’s Alpha if Item Deleted của mục quan sát là đáng kể từ 0.3 trở lên. Chúng ta sẽ loại mục quan sát đó để tăng thêm độ tin cậy của thang đo.
3. Phân tích độ tin cậy Cronbach’s Alpha trong SPSS
Một nhà nghiên cứu đã đưa ra một bảng câu hỏi gồm sáu câu hỏi để đo lường mức độ hài lòng của các sinh viên với một khóa học trải nghiệm thực tế. Mỗi câu hỏi được thiết kế với thang Likert 5 điểm từ “rất không đồng ý” đến “rất đồng ý”. Để hiểu được liệu các câu hỏi trong bảng câu hỏi này có đo lường một cách đáng tin cậy cùng một biến tiềm ẩn (sự hài lòng) hay không, Cronbach’s alpha đã được chạy trên SPSS với cỡ mẫu gồm 15 sinh viên.
– Bước 1. Nhấp vào Analyze> Scale> Reliability Analysis …

– Bước 2. Trong hộp thoại Reliability Analysis, bạn chuyển các biến từ Item1 đến Item7 vào trong hộp Items.
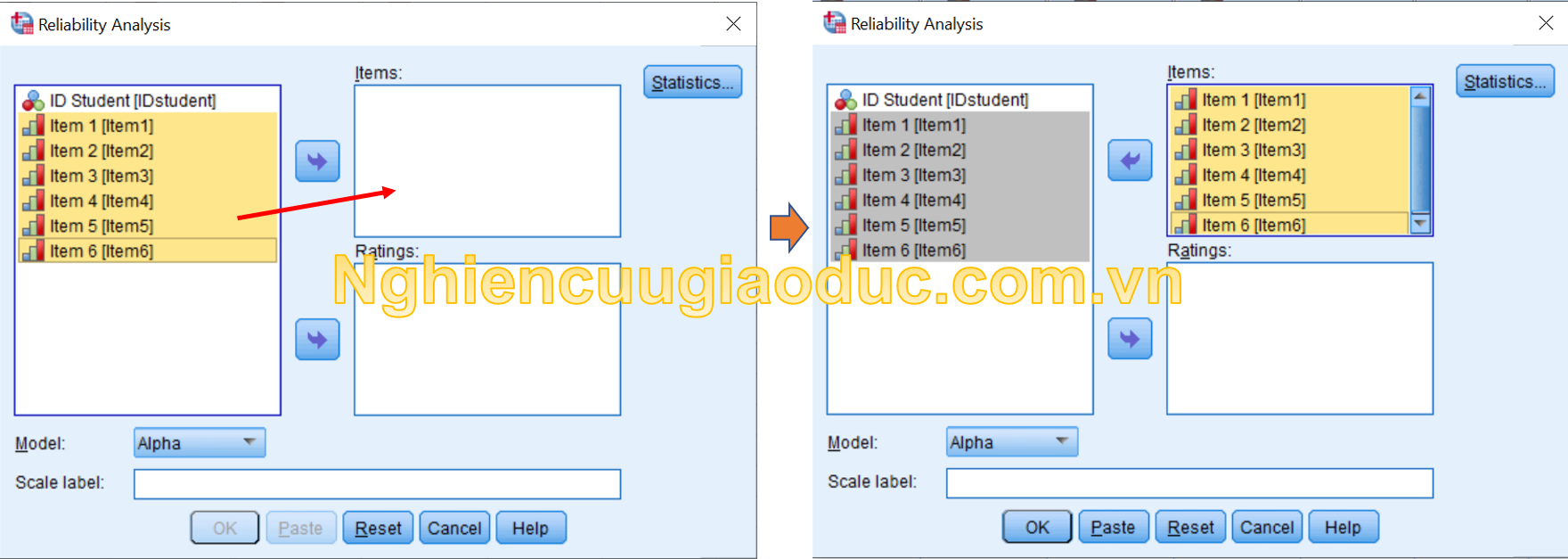
– Bước 3. Nhấp vào nút Statistics để mở hộp thoại Reliability Analysis: Statistics. Chọn Scale if item deleted để kiểm tra thang đo nếu loại bỏ biến. Sau đó nhấp vào Continue.
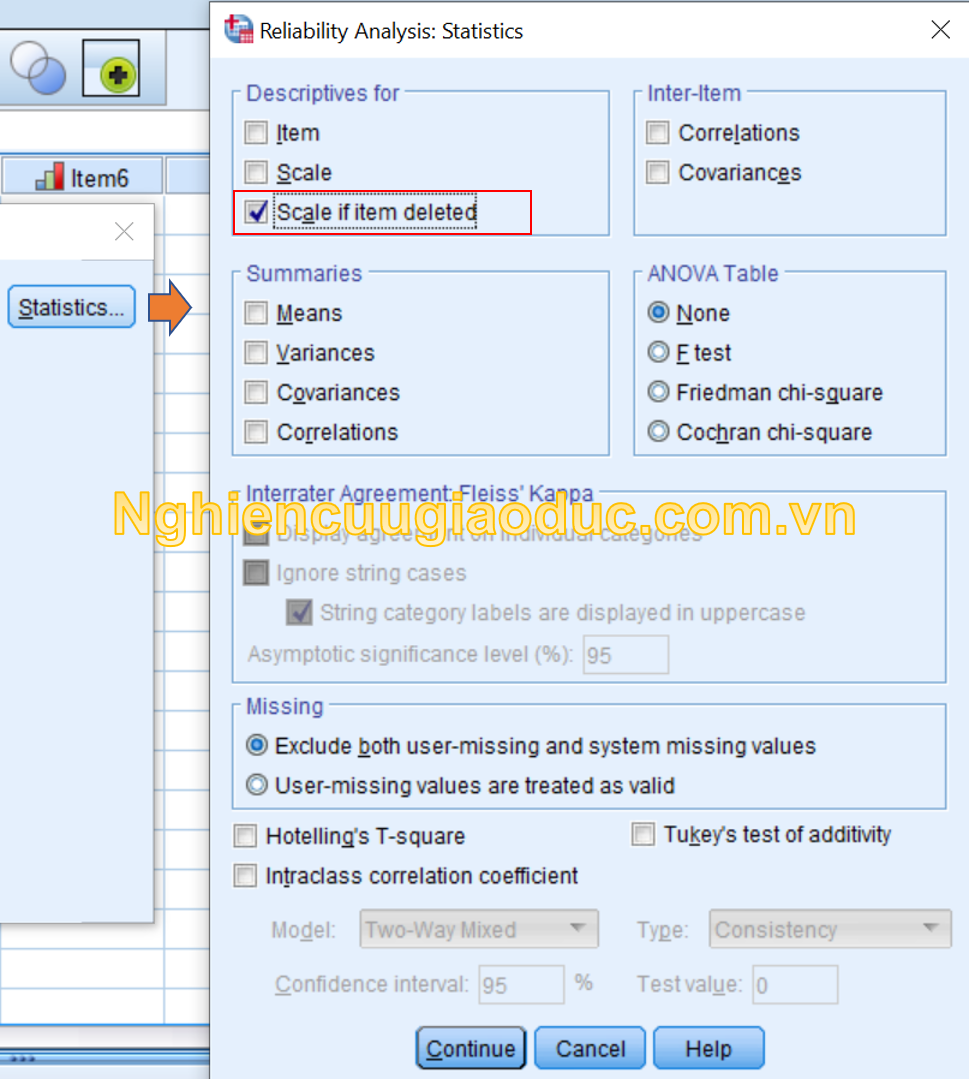
– Bước 4. Nhấp vào OK để chạy kết quả.
Phân tích kết quả:
SPSS sẽ chạy ra một số bảng kết quả, tuy nhiên chúng ta chỉ cần tập trung vào hai bảng quan trọng dưới đây:

– Bảng Reliability Statistics cung cấp giá trị thực tế của Cronbach’s alpha. Trong ví dụ này, chúng ta nhìn thấy Cronbach’s alpha là = 0.841 (> 0.7), biểu lộ một mức độ cao của độ tin cậy nội bộ cho thang đo.
– Bảng Item-Total Statistics cung cấp các thông tin quan trọng về hệ số tương quan biến – tổng ‘Corrected Item – Total Correlation’ và Cronbach’s alpha nếu biến bị xóa ‘Cronbach’s Alpha if Item Deleted’. Kết quả kiểm định cho thấy các biến quan sát đều có hệ số tương quan biến – tổng phù hợp (≥ 0.3). Vì hệ số Cronbach’s alpha ≥ 0.7 và giá trị hệ số tương quan biến – tổng ≥ 0.3 nên chúng ta không cần xem xét giá trị của cột ‘Cronbach’s Alpha if Item Deleted’.
Viết kết quả trong báo cáo khoa học: Một bài kiểm tra Cronbach’s Alpha đã được thực hiện để kiểm tra độ tin cậy nội bộ của thang đo mức độ hài lòng của các sinh viên trong khóa học trải nghiệm thực tế. Kết quả kiểm tra Cronbach’s Alpha cho thấy các biến quan sát đều có hệ số tương quan tổng biến phù hợp (≥ 0.3) và hệ số Cronbach’s Alpha = 0.841 (> 0.7) nên thang đo đạt yêu cầu về độ tin cậy nội bộ.
Tài liệu tham khảo
[1] Cortina, J. M. (1993). What is coefficient alpha? An examination of theory and applications. Journal of Applied Psychology, 78(1), 98–104. https://doi.org/10.1037/0021-9010.78.1.98
